3. Trigonometry
d. Trig Identities
6. The Triangle Inequality
Given a triangle with side lengths \(a\), \(b\) and \(c\), then: \[\begin{aligned} |a-b| \le c \le a+b \end{aligned}\] \(\Leftarrow\Leftarrow\) Read it! It's animated.
Consider a triangle with sides of lengths \(a\), \(b\) and \(c\). We will hold the lengths of \(a\) and \(b\) fixed while the angle between them changes. Then the length \(c\) changes.
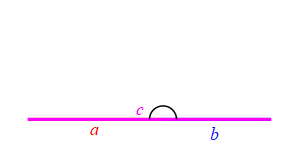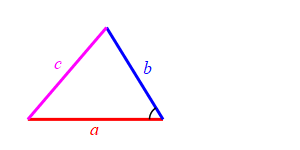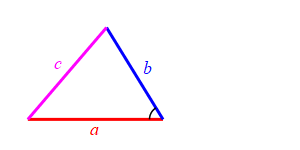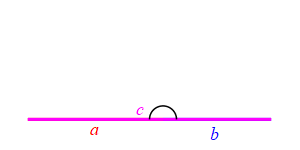
When the angle between sides \(a\) and \(b\) is very small, side \(c\) approaches \(|a-b|\) but always stays larger than this as long as the angle is non-zero. So: \[ c \ge |a-b| \]
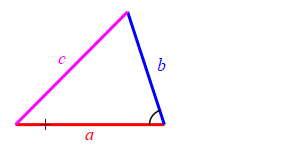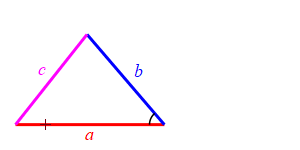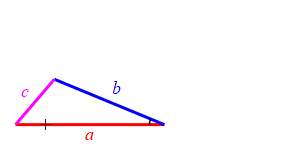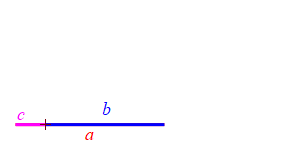
Because we don't know which is bigger, \(a\) or \(b\), and \(c\) must be bigger than the positive difference. The figure above has \(b \lt a\). The figure at the right has \(b \gt a\).
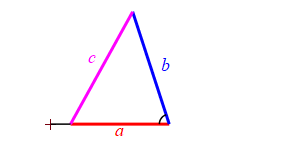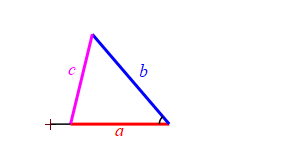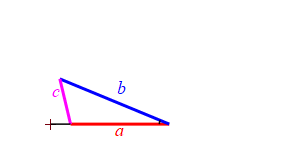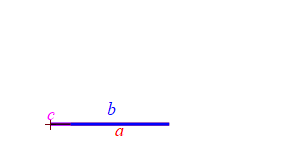
When the angle between sides \(a\) and \(b\) is very large, side \(c\) approaches \(a+b\) but always stays less than this as long as the angle is not \(180^\circ\). So: \[ c \le a+b \]
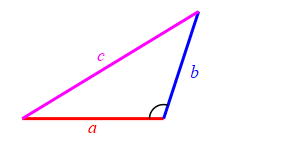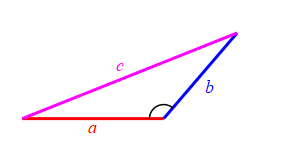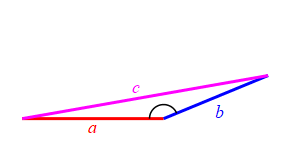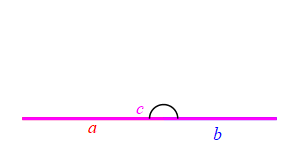
Together we have \[ |a-b| \le c \le a+b \]
Given three positive numbers \(a\), \(b\) and \(c\). If \(c\) is the largest
and \(c \lt a+b\), then there exists a triangle with sides \(a\), \(b\)
and \(c\).
\(\Leftarrow\Leftarrow\) Read it! It's easy.
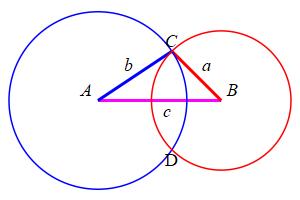
Draw a line segment \(\overline{AB}\) of length \(c\).
At the end \(A\), draw a circle of radius \(b\).
At the end \(B\), draw a circle of radius \(a\).
Since \(a+b \gt c\), these circles must intersect at two
points \(C\) and \(D\). Then the triangle \(\triangle ABC\) has sides
\(a\), \(b\) and \(c\).
In each problem, is there a triangle with sides \(a\), \(b\) and \(c\)?
-
\(\quad a=3 \qquad b=4 \qquad c=6\)
Correct! Since \(6\) is the longest side and \(6 \lt 3+4\), there exists a triangle with sides \(3\), \(4\) and \(6\).
Incorrect! Since \(6\) is the longest side and \(6 \lt 3+4\), there does exists a triangle with sides \(3\), \(4\) and \(6\).
-
\(\quad a=3 \qquad b=4 \qquad c=8\)
Incorrect! Since \(8 \gt 3+4\), a triangle with sides \(3\), \(4\) and \(8\) would violate the Triangle Inequality.
Correct! Since \(8 \gt 3+4\), a triangle with sides \(3\), \(4\) and \(8\) would violate the Triangle Inequality.
-
\(\quad a=9 \qquad b=2 \qquad c=6\)
Incorrect! Since \(9 \gt 2+6\), a triangle with sides \(9\), \(2\) and \(6\) would violate the Triangle Inequality.
Correct! Since \(9 \gt 2+6\), a triangle with sides \(9\), \(2\) and \(6\) would violate the Triangle Inequality.
-
\(\quad a=7 \qquad b=2 \qquad c=6\)
Correct! Since \(7\) is the longest side and \(7 \lt 2+6\), there exists a triangle with sides \(7\), \(2\) and \(6\).
Incorrect! Since \(7\) is the longest side and \(7 \lt 2+6\), there does exists a triangle with sides \(7\), \(2\) and \(6\).
-
\(\quad a=4 \qquad b=10 \qquad c=7\)
Correct! Since \(10\) is the longest side and \(10 \lt 4+7\), there exists a triangle with sides \(4\), \(10\) and \(7\).
Incorrect! Since \(10\) is the longest side and \(10 \lt 4+7\), there does exists a triangle with sides \(4\), \(10\) and \(7\).
-
\(\quad a=4 \qquad b=12 \qquad c=7\)
Incorrect! Since \(12 \gt 4+7\), a triangle with sides \(4\), \(12\) and \(7\) would violate the Triangle Inequality.
Correct! Since \(12 \gt 4+7\), a triangle with sides \(4\), \(12\) and \(7\) would violate the Triangle Inequality.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum